波動は、複素数で記述される物理量としてよく知られています。中山の携わる分野では、量子力学で現れる電子の波動方程式、回折理論、交流インピーダンス法など様々です。しかし、なぜ「虚」なる数が現実の自然現象を記述するのに使われるのかイマイチ分かりにくいと考える化学系の人は多いのではないでしょうか？　で、もちろん僕もその一人です（でした？）。　ここでは、中山の足りない知識で精一杯（のつもり）、複素数による波動の記述について説明しようと思います。といっても、例によって勘違いなどはあると思うので、その辺は穏やかに指摘してください。
　なお、多くの人は複素数の概念自体を高校生のときに勉強したと思われますが、カリキュラム改訂で複素平面を勉強した人もいれば無い世代（中山がそう）もあるので、かなり簡単なところから説明したいと思います。
（更新履歴）　学部の授業ノートを元に初版作成 (2008/12/28)

虚数という概念を導入することは、現代人でも得体の知れないものを受け入れなければならない抵抗を感じるのではなかろうか？　でも、これと同じような葛藤が負数の導入のときにもあったと考えられている。ギリシア時代には、地球のサイズの測定や、ユークリッド幾何学の完成、原子論まで成し遂げられたが、そのギリシア人でさえも負数の概念の導入はどうやらできなかったようである。実際に、ヨーロッパでは１７世紀に至っても一部の著名な数学者にすら受け入れられないような状況であり、「－1個のりんご」という概念がつかめなかったと考えられている。
しかし、現代人であれば（平均的な大学理系の人であればなおさら）「－1個のりんご」というのは、もちろん現実の現象ではないけれど、計算を容易にする単なる抽象概念としての負数だということは分かる。ここで「抽象概念」という言葉が重要であって、数学というのは現実になくても論理さえ完結すれば（無矛盾であれば*1)、そのまま現実を無視して議論を進めて差し支えないのである。しかも、負数を導入しても（適切な数学体系を選んでさえいれば）物理現象を（今のところ矛盾に遭遇せずに）記述できるので、「便利だから」使っているというのが中山の理解である。
話は回りくどくなったが、歴史的に数を考えていくと、ギリシア人（から１７世紀のヨーロッパ人*2）の考えていた数直線というのは、図１のような正数だけを考えた数直線である(*3, *4)。そしてその後、図２のような負数も考慮したような数直線が出てきたわけだ。　ここまでは現代人にも、そんなに抵抗なく（？）理解できる部分である。(*5)

実は、複素数の導入はもう一歩踏み込めばいいのであって、数直線（一次元）上に展開された実数を平面（2次元）に広げるという点がポイントである。すなわち、図３のように、数直線に対して直角方向に虚数軸を設定すると言うことである（図３に示した平面を複素平面・ガウス平面という）。　ここで、数直線に直角に交わるような数の存在を、ＳＦチックに異次元空間とからめて想像する必要は無い。
この複素平面導入のポイントは、つまり2変数で表される物理量などを一つの数字として取り扱えることである。たとえば、図3に赤い矢印で示したベクトルは、一つの数字 a + bi で記述することが出来る。。。。　そんなことだったら、2変数のxy座標(デカルト座標)を使えば、変な虚数の概念なんか登場させることなく実数だけで記述できるじゃないかと言われそうだけど、複素平面を導入すると2つの実数を使わなくても、一つの複素数で平面上の点を表せるので、代数計算が簡単になる場合がある。その典型的な例が、波動の重ね合わせを記述する場合で、デカルト座標系を用いて議論するよりも複素平面を導入したほうが計算が容易なのだ。だから、波動を取り扱う分野（回折理論とか交流インピーダンス法とか）では、イマイチ分かりにくい複素表記で式が論じられている教科書が多い。もちろん、実数だけを用いたデカルト座標系で、波動を取り扱うことも可能なのだが計算が面倒になるから使っていないということである。ということで、次のセクションでは複素数平面上での代数計算について紹介する。

*1 しかし、無矛盾であることを数学自身は証明できないのではあるが・・・（たぶん、ゲーデルの不完全性定理？？）
*2 インド人、中国人はかなり早く負数の概念を導入していたようである。
*3 まだ、この時代には数直線の完備性は得られていない。無理数が有理数と本質的に異なるクラスの数であることはカントールによって説明されている。
*4 あと、何気に図中に記述した無限大の概念もユークリッドの時代には直感的に理解されていたが、その定義づけは同様にカントールが現れるまでよく分かっていなかった（はず）。
*5 現代人が過去の人に比べて優れているというわけではないのだが、私達は初等教育の段階で負数や無理数の存在を（厳密な証明抜きに）勉強させられているので、素直にその存在を受け止めることができるという下地が出来ている。その意味で、教育法やカリキュラムの進歩に拠るところが大きいのかもしれない。

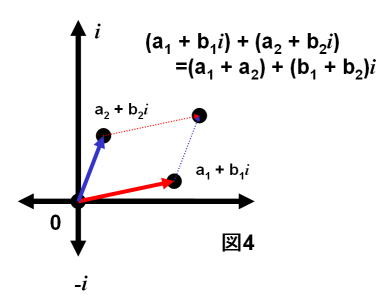
複素数の代数演算は、基本的に実数で学んだそれの延長線上にあると考えてよい。i ²=-1というルールさえ覚えていればＯＫである。したがって、加法は図４に表されるとおり、実部と虚部を別々に足し算すればよい。これは丁度、デカルト座標系で言えば、(a1, b1), (a2, b2)で表される数のベクトル和と同じ操作をしたことになっている。

これくらいだと、あまり複素数を導入したことに対するご利益を感じないわけだが、乗法ではすこし話が違ってくる。だが、乗法を説明する前に複素数を学ぶ上で外すことの出来ないオイラーの公式について説明しよう。オイラーの式とは、こうだ。

でも、式だけでは直感的な意味合いが分からないので、複素平面上で説明をしよう。図５を見てもらうと、図３で赤線で示したベクトルに対して、その長さを r、なす角を θとしたときに、 (a + b i) は、r (cosθ+ i sinθ)で表される（高校のときに習ったcosやsinの定義から明らかだと思うのですが？）。 実は、これは指数関数表記で表すことが出来ますよと言っているのがオイラーの公式で、r・exp(iθ)は赤線のベクトルと等しくなるのである(*6)。　もうお分かりのように、ｒやθで座標を示すやり方を極座標表示というわけだがオイラーの公式は簡単に(x,y)座標系と極座標形式を変換できる公式でもあるのだ。

この立場から、乗法を考えてみると、複素数のありがたみがよく分かる。図５で示した赤線のベクトル 　ｒ・exp(iθ）を２乗してみよう。そうすると、図６の上の式に示したように、r²×exp(2θi）となる。極座標的な考えによれば、ベクトルの長さｒは２乗になり、なす角は2倍になるということを示している。実数だけを取り扱っていたときには、われわれは exp(iθ)＝１（なぜならθ=0だから）のケースだけを想定していたわけだが、複素数の場合には乗法の概念は拡張されて、「なす角θの回転」という操作が加わることがここで明らかになる。

以上で見てきたように、複素数で示された四則演算の規則は、従来の実数数直線上で体系化された四則演算のルールを損なうことなしに、極座標形式との変換を容易にし、また乗法における回転という概念を追加することに成功したものだと考えてもいいのではないかと思う。


*6 何でオイラーの公式が成立するのかは、今日の中山には分かりません。（過去あるいは未来の中山は知っていた（いる）かもしれませんが）

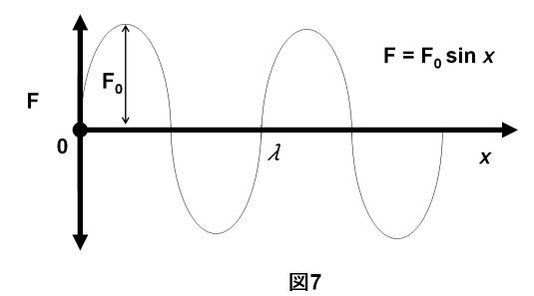
今までのわずかな複素関数の知識を元に、目標である波動を複素数表記していく方法とコンセプトを紹介しよう。まず、一般に波動だけど、一番ポピュラーな波動は正弦波である。つまり、図７に示したようなsinの関数の波のこと(*7)。ここでは、振幅をＦ0、波長をλとしている。ｘは位置を示す変数ということでもいいのだけど、時刻ｔでも値Ｆは刻々と変っていきます。位置ｘにおけるＦの正確な値を知ることはあまり意味がない。いずれにしても、図は、ある一瞬（時刻　ｔ）の時の波動の様子を示したと思ってくれれば、今のところＯＫだろう。

で、高校の物理の授業（インピーダンスとか出てきたあたり）で習ったかと思うのだけど、この波動は極座標形式でも示すことが出来る（図８の左側）。　更に言うと、せっかく極座標にするので複素平面で記述しましょうというのが、今後の議論のミソになる。　図８で示したように、波動（一波長分）は左側の極座標系で一対一対応することが出来る（a～eの点が両者で一対一対応していることに注意）ので、容易に両者を変換可能です。従って正弦波の場合、極座標形式ではF = F₀ exp(iθ)として波動を表すことができる。ここで、振幅Ｆ₀は極座標形式ではベクトルの長さに該当し、座標x とθの関係は、２π＝λの関係から、θ= 2πx/λとすればよい。

*7　別に物理現象として現れる波が正弦波になる必要はないのだが、フーリエ変換によって全ての周期関数はsin波（とcos波)に分解できるから、正弦波は重要（だと思う）。「フーリエ変換とは何？」と問われると、これはまた別の機会か、よそをあたってくださいといつものように言い逃れをすることになります。あしからず。

今まで長々と複素数について長々（？）と述べてきましたが、最後に結論的に述べたいことは、（中山的には）ただ一点。複素数表記を使うと、「位相のずれた波の計算が簡単だということ」です。その例として、回折法で問題になる合成波の計算を例に説明しましょう。

Ｘ線回折の測定で、ある基準となる回折面に対して、異なる回折面で散乱されたＸ線を考えた場合、その散乱Ｘ線の振動は相対的に横にずれることになる（図９参照）。　

このとき波はｘ座標系でΔｘ、極座標系ではΔθずれることになるが、その時の値は光路差の計算から算出することができる（ここでの議論とは関係ないので割愛、たとえばこのページを見てください）。とにかく、ΔｘあるいはΔθずれたときの合成波の計算をしてみる。　まずは、正弦波の形式で合成波の計算を試みようとすると･･･

式は簡単なのだが、問題はsin(x+Δx)の項なのである。これを展開するには、高校時代にならった三角関数の加法定理（さいた～コスモス～♪）を思い出さなければならず、かなりメンドクサイ。（これを、全ての回折線に対して和をとるような一般式を考えようとすると頭がイタイ）

ところが、極座標形式の場合は指数関数なので、すいすい計算ができる。

ってことで、この式から容易に合成波の特徴が分かる。最後の（exp iθ）というのは、波の基本式である。大事なのはその前の部分で、F0x{1+exp(iΔθ)}が波の振幅に相当する。Δθは位相差で光路差が決まれば一義的に決まる（定数になる）部分である。従って合成波の振幅（これが物理的には重要な意味がある）を考えると、位相がΔθずれると、２つの波の振幅は2倍にならず、基準の波（式中では「１」で表された部分）に対してexp(iΔθ）倍した振幅の寄与しか与えないということが分かる。
中山の別のホームページでＸ線回折の理論を述べているが、その一般化された散乱方程式は下記の式のとおりで、指数関数の部分（ exp (なんたら））の中身は、基準散乱波に対する注目する散乱波の位相差を算出しているのに相当している。で、それを全部足し合わせる（この場合積分している）ことで、合成波の記述が一般化できるということを意味していたのである。

なお、これで散乱方程式の記述については、だいたいＯＫなのだが、われわれが実際に観測する物理量との関連で、複素数の計算法も記述しておきましょう。Ｘ線回折の場合は、波を直接図るのではなく（マイナスの振幅というのはディテクターで検知できない）強度を測ることになる。強度は波の振幅の２乗になるとことのは物理の教科書に書いてあると思うのだけど、その複素数表記の場合、2乗の計算法の意味は単純に(a+bi)2ではないので注意が必要だ。複素数の場合は、波の強度を出す場合に共役複素数を掛け合わせるのがルールなので、 (a + bi)に対して、(a - bi)を掛け合わせるようにする。従って、a2+b2が答えになるので、注意しよう。（でないと、いつまでも物理量の中に虚数項が残存してしまうことになる）　（極座標形式の場合は ベクトルの長さr2を求めていることに相当する・・・）。

ということで、虚のイメージが胡散臭げな複素数が、波動という物理現象を記述する場合においてとても役に立つことを、簡単に説明した（つもりである）。交流インピーダンス法とか、量子力学で出てくる波動方程式もその延長です（たぶん）。ってことで、それ以上のことは中山はよく分からないし、そろそろ字を書くのにも飽きてしまったので、参考書なり、賢そうな先輩（時には後輩）を見つけて尋ねるようにしましょう。でわ。