交流インピーダンス法の用途は幅広い。中山の関与する範囲の研究分野でも、電気化学反応の反応速度論解析、イオン導電率の測定、誘電率の測定に応用できる。ここでは、イオン導電率を例にとって、交流インピーダンス法の原理の説明を試みる。測定原理の基本は、「時間分割」である。

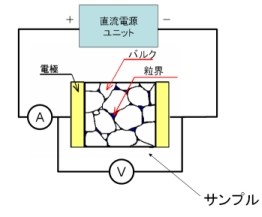
交流インピーダンス法の話の前に、測定する側になるセラミックス材料のイオン導電体について紹介しよう。リチウムやフッ素などのカチオンやアニオンは結晶やガラスのようなセラミックス固体の中でも、適当な結晶・分子構造を持っていれば溶液のように移動することができる（イオン伝導）。そうなると科学者の人情としては、電流電圧計を用いて伝導率という形で定量的に値を計りたくなる。単純に考えれば、図１のような方法が思いつくはずだ・・・。なぜなら、そうするば電圧計の値を電流計の値で割れば、オームの法則から抵抗値が求まるから。

　しかし、サンプルをよく見てみると、セラミックスの焼結体中のイオン拡散の抵抗成分は様々な成分から発生していることがわかる。つまり図２に示すように、１）粒子バルク内イオン伝導に由来するもの、２）粒子と粒子の接触界面（粒界）での伝導に由来するもの、３）そして電極とサンプル界面でのイオン伝導（またはブロッキング）に由来するものである。

　直流法ではこれらの抵抗成分を区別することはできないから、全ての抵抗値の和となる。でも（大抵は）バルクのイオン抵抗だけを抽出したいから、とても悩ましい問題に直面する。

　ということで直流でイオン伝導の測定をしても、３つの成分を全て含んだ形でしかデータが手に入らないという問題に直面してしまうわけだが、どうにかして分離したいのが人情であろう。それでは、バルク内部、粒界、電極界面でのイオン伝導に依存する変数は何かないかということになる。これが、「時間」という変数になる。もう一度図１のような回路を使って定電圧を引加してイオンを流す実験を考える。しかし今度は新たに時間に対する抵抗の変化を考える。そうすると、図３のような変化が得られる。
　時間０で電圧を０からEに設定すると、図１のサンプルの場合、バルク抵抗Rb, 粒界の抵抗 Rgb, 電極界面の抵抗 Reiの和に対応として電流が流れると考えられるが・・・実際にはイオンの応答速度が異なるので時間に対応して抵抗値に変化が見られる。
　例えば、バルクのイオン伝導は電場にたいして応答が速いから、比較的短い時間でイオン伝導に由来する抵抗が観測される。ところが、粒界部でのイオン伝導は、バルクのイオンの動きに比べるとモタモタしているから（この表現は適切かどうか分からないけど）、もう少し時間がたってからじゃないと抵抗成分が観測されない。電極界面はもっと遅い。・・・・・ということで、お分かりのように理屈上は図１のような装置を作って、時間に対して電流値をプロットしていけば３つの抵抗成分を分離できるはずである。
　・・・・ところが、水を差すようだけど現実は厳しくて、この時間スケールがマイクロ秒とかミリ秒とかになってしまう。つまり、技術的に測定が難しいのだ。まさかストップウォッチを使って測定するわけにも行かない。。。。。

　とまぁ問題はここでは技術的なレベルまで解決したわけではない。でも原理的には、時間を関数にすれば抵抗成分を分けることができる。これが「時間分割」のコンセプトであって、一番強調したいことなのだ。で、イオン伝導に関わらず、様々な素過程反応を含む化学反応もそれぞれの反応は特有の応答時間があるから素過程反応を分離することができたりできる可能性がある。

抵抗成分を分離することに関して、原理的には時間依存性を調べることで分離可能であることが分かった。あとは、技術的な課題が残っただけである。結論から述べると、それを解決したのがこのHPのテーマである交流インピーダンス法になる。（大分、前置きが長かったねぇ・・・。性格なんです。）19世紀後半から今世紀にかけてKohlrausch, Warburg, Krugerらによって提案された。
　直流法ではできなかったけど、交流法で時間分割ができるのは周波数を変化させながらインピーダンスZ*(=Z'+iZ'') （つまり抵抗のこと）を測定できるからだ。その周波数レンジは上限が10MHzまでできるから、その逆数の0.1マイクロ秒くらいの抵抗値の変化を追うことができる。もう少し詳述しよう。例えば試料に高周波電場を印加した場合、緩和時間の小さい伝導成分は電場の変化に応答できるが、緩和時間の大きい伝導成分は電流が流れる前に逆の電場が印加されるため交流電場の変化に追随することができず、結果として緩和時間の小さい抵抗成分のみを抽出できる。セラミックス焼結体のイオン伝導の場合、緩和時間は経験的に（ バルク＜粒界＜電極界面 ）の順で小さいことが知られているため、周波数に対してインピーダンスをプロットするとBode線図と呼ばれる図４のようなグラフが得られる。図４(a)は周波数に対してインピーダンスの実数部Z'（すなわち実抵抗）をプロットしたもので、平坦な段が2つ観察されるが、これが各抵抗成分の抵抗値を示している。図４(b)は虚数部Z''をプロットしたもので交流電場に応答する抵抗の位相遅れに対応している。

　交流インピーダンス測定によって得られたデータを見てみると、１）測定周波数、２）インピーダンスの実部Z'、３）虚部Z''の３つデータが得られる。（装置やソフトによっては、インピーダンスを極座標でアウトプットすることもあるのでそれはよく確認する。）　で、図４みたいなBode線図でインピーダンス解析をしてもいいのだが、実際にはBode線図で解析するのは難しい。これは、現実には図４みたいな抵抗が一定の部分はほとんど表れないからである。だから、実数成分を横軸に、虚数成分を縦軸にプロットした「複素インピーダンスプロット」で表すのが普通である。そのとき、必ず実軸と虚軸の値のサイズは同じくしないといけない。
　インピーダンスプロットは、イオン導電体を測定するか、誘電体を測定するかという測定対象によって色々な形になる。ここでは引き続き、イオン導電体の例で複素インピーダンスプロットを見てみる。（図５）　複数の半円状のプロットがあらわれるが、この円弧の直径がバルク、粒界のそれぞれの抵抗となる。

　複素インピーダンスプロットから簡単にRが求まればいいが、現実にはそれぞれの抵抗成分の緩和時間（応答時間）が近いと円の分離も難しい。そこで、データ解析の王道であるフィッティングにより有用な数値を得ようとする。そのためには、フィッティングのモデルが必要となるわけで、よく知られた電気回路の成分を使って「等価回路」を作る。等価回路でよく使う組み合わせはRC回路で、Rは抵抗、Cはコンデンサーを意味する。コンデンサーのCはいささか分かりにくいかもしれないが、これは応答遅れを意味する。図２を使って説明したように、それぞれの抵抗成分は固有の応答時間（緩和時間）を有している。その電場変化に対応する応答遅れをコンデンサー成分で代用していると考えればいい。コンデンサーのキャパシタンスCが大きいほど、電流を流す前にコンデンサーで電荷を溜めてくれるからその分だけ応答が遅くなる。このCは抵抗成分固有の応答時間に対応するので、経験的に抵抗成分がどのような現象に由来するのか推測するのに便利である。なんで、応答時間で代用しないのかというと、キャパシタンスCは温度に対してほぼ一定であるためである。緩和時間は温度に対してアレニウス型、つまり指数関数的に変化してしまうので使いにくい。ただしキャパシタンスはサンプルの幾何パラメーター（つまり試料厚みや電極面積）に依存するので、極端に小さい・大きいサンプルを作った時は注意しないといけない（といっても、桁単位で大きく値が変化するとは思えないわけだが・・・）。
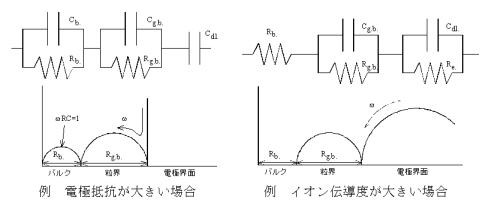
　それぞれのRC回路の複素インピーダンスプロットを図６に示してみよう。RとCを並列につなぐと半円になることが分かるだろう。　また、イオン導電体のインピーダンスプロットの考えられる幾つかの例を図７に示した。いつも図５のようにはならないので、臨機応変に対応することが必要である。例えば、ガラスの場合は粒界がないから粒界のRC並列回路はフィッティングから除くなどである。
　で、適当なフィッティング回路を作ったら、あとは適当な初期値を与えてフィッティングするのみである。グッドラック！

そろそろ僕は疲れたのでこれで話を一旦やめてしまいたい。僕はそれなりに忙しいかったりするし、そもそも怠け者なのだ。時間分割のコンセプトが分かれば、後は適当な教科書を読めばいい気もする。最後に等価回路のフィッティングで簡単なメモを残しておこう。

１）　関係式

　緩和時間τについて、　f(top)は半円の頂点の対応周波数、

２）　ワールブルグインピーダンス

　低周波数側で、傾き４５度の直線が現れたらそれはワールブルグインピーダンスという。これは普通電極内でのイオンの拡散に由来すると言われている。電気化学の教科書に掲載されているのでチェックしてください。

３）　キャパシタンスの経験値

イオン伝導の場合（リチウムイオン）
　・バルク中のイオン伝導：　ｐFオーダー
　・粒界：　ｎFオーダー
　・電荷移動：　μFオーダー

もっとも、そんなに当てになる数字ではない。

４）　つぶれた半円

逆にキレイな半円になる場合は、緩和時間（応答時間）が１つしかないという仮定（デバイ・モデル）に依拠している。もし、素過程が複数あって、その緩和時間がとても近い場合は、円が複数重なってつぶれた半円になる。この場合の解釈法として
　（１）円の中心をずらして、α角で評価する。（下の図）
　（２）CPE (constant phase element)を使って評価する。
などの方法がある。詳しくは教科書なんかを読めばよい。回路を変化させることに根拠はほとんどないと思っていいだろう。便宜的な方法。