X線吸収分光 (XAS, XAFS, XANES, EXAFS)

XAFS -> X-ray Absorption Fine Structure -> X線吸収微細構造
XAS -> X-ray Absorption Spectra (=XASF) -> X線吸収スペクトル

XANES -> X-ray Absorption Near Edge Structure -> X線吸収端近傍スペクトル
NEXAFS -> Near Edge XAFS (=XANES) -> 吸収端近傍XAFS

EXAFS -> Extended X-ray Absorption Fine Structure -> 広域XAFS

XAFS(=XAS) = XANES(NEXAFS) + EXAFS

このよく分らない式の意味は後で説明する。

(2004/11/16)
一概にX線吸収スペクトルといっても、その実験法は透過法・蛍光法・全電子収量法など沢山ある。だけど、まずポイントをつかむために透過法を引き合いにして説明をする。実験そのものは簡単で、下の図のようにサンプルにX線をあてて、透過したX線を調べるテクニックである。

では原子レベルでは何が起こっているのだろうか？それを示したのが下の図である。入射Ｘ線は内殻電子を励起し光電子にする。透過Ｘ線は光電子に励起さ れた分だけ強度が減る。 また内殻の軌道エネルギーは元素種毎に固有の値を持つので、スペクト ルは元素種別の情報を与える。

更に励起した光電子は波の性質を持つので、球面波状に広がる（下の図）。 隣接した原子に球面波は散乱され波同士が干渉する。 透過波はこの光電子発生・散乱・干渉の情報を含んでいる。なお、この散乱という現象に対して散乱理論という学問領域がある。

つまり、得られるスペクトルは内殻電子が励起し外殻軌道に遷移するか、あるいは自由電子のようになった光電子が周囲の原子に散乱されるような過程を反映した結果が得られる。

最後に、実際の実験の様子を下に示す。サンプルの前後に、X線光路に沿って入射X線と透過X線の強度を測定し、吸収スペクトルを得ている。X線は単色化（波長を揃えること）されている。

(2004/11/16)

入射Ｘ線が内殻電子を非占有軌道以上に励起するエネルギー以上のフォト ン(E=hf)を有するとき吸収が観測される（下図（右）のＡの領域）。逆にそれ以下の エネルギーしかない場合は電子は励起できないので吸収は見られない（下図（右）のＢの領域）
不正確な説明だが第一近似として、ＸＡＮＥＳは光電子が原子の電子束縛 ポテンシャルから抜け出せず非占有軌道に励起する過程を反映したスペク トル。ＥＸＡＦＳは光電子が隣の原子まで飛行し散乱・干渉する過程を含んだスペクトル。明快な境界線はなく、おおよそ波数ベクトルで3～4/A^-1あたりが境目になる。 （ＸＡＮＥＳも散乱理論の枠内ではＥＸＡＦＳと理論は全く同じで取り扱える。）

(2004/11/16)
XAFSは特定元素の非占有軌道の情報を与える。 では非占有軌道のLDOSと同じなのか?　これは、 ある程度まではそのように考えて差し支えないだろう。ここでは、その過程に沿って話を進めよう。しかし多くの場合はこの考え方が成立しない。このことはいつか詳述する。

ところで、XAFSのスペクトルは非占有軌道全てを表すのではない。選択側に従った 許容遷移の情報が得られる。 分光学的選択則*では、副量子数が±１の変化をしないといけないので、 例えばs(l=0)軌道から励起した電子は必ずp(l=1)軌道に遷移する。したがっ てp軌道のLDOSがXANESでは与えられる。（対称性の低下、混成軌道の形成は微弱な禁制遷移（すでに禁制ではないのだが）を生じる。多くの場合、 これらの情報は有用であるが解釈は困難であるのでここでは取り扱わない） 

*一番簡単な説明は、フォトンの角運動量が１なので遷移時は角運動量保存の法則に従い副量子数の変化が要求される。

(2004/11/16)

ペロブスカイト中のNb L3-edge（下の図）。下は酸化数５のもの、上は酸化数が４に近 づいたもの（４ではない） L3なのでd軌道の非占有軌道に対応するスペクトルを与える。Nbは八面体 結晶場によりt_2g, e_g分裂を起こす。したがってスペクトル中に見られる二つ のピークはt_2g, e_gに対応する。還元するとt_2gに電子が入り非占有軌道が減少する。そのため、図のスペクトルは還元とともにt_2gのピーク強度が減少す る。

先ほどと同じサンプルのNbのK-edge。Nbの5p軌道を反映している。d軌道 は局在化した軌道なのでピークエネルギーのシフトに関する情報が乏しい 傾向があるが、pは非局在化した軌道なので酸化数変化の影響を大きく受ける。カチオンの場合、高価数になるほど静電場の影響で電子を束縛する 傾向が強くなるので励起するためのエネルギーが大きくなる。そのため、 ピークは高エネルギー側にシフトする。 
・・・・と書いたが、この説明は正確には誤りと思われる。遮蔽効果などを考え合 わせると、別に静電場で高エネルギー側にシフトする必要はなく、実際に計算によっても逆に低エネルギー側にシフトすることも考えられる。ただし経験則としてはほとんど例外なく上記のような現象が観測されるのでこの覚え方は有用。リファレンスサンプルを用いて酸化数をチェックすることを進めるが、 この場合もスピン構造・結晶構造により有効でないこともある。また、ピークシフトを第一原理MSで予測することもほとんど困難。

☆XANESの吸収強度のノーマライゼーションについて、最大強度＝１という解析が散見されるがこれは誤り。基礎吸収で規格化しないといけない。細かい流儀は多々あるが、例えば任意のエネルギーでの基礎吸収強度を１としてもいいし、基礎吸収線を延長してE0（吸収端エネルギー）のところの強度を１としてもよい。

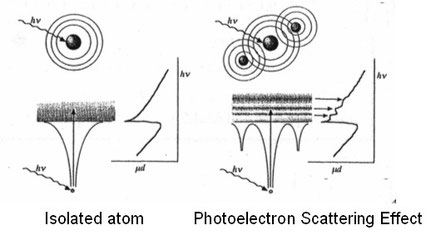
EXAFS振動に対応するスペクトルについて詳述する。XANESより大きなエネルギーのX線が入射した場合、光電子は隣の原子まで飛行した結果の情報を与える。この光電子（波の性質を有する）は球面波状に周囲に広 がる。もし、隣に原子が無い場合（真空中で孤立した原子の場合）は、のっぺりしたスペクトルを与える（上・左の図）。一方、上・右の図のように光電子波が周囲の原子に当たると光電子の散乱が起きる。散乱はＸ 線回折と同じく前方で強く散乱し後方で弱く散乱する。また、散乱された波同士で干渉が起こり、スペクトルは光電子エネルギーに対して波打った特有 のスペクトルを与える。この振動スペクトルを解析することで、局所的な原子の配列に関する情報が得られる。

その１：実際のEXAFS信号の抽出の仕方。 上の図は生スペクトル。緑色の線はバックグラウンドなので差し引く（バックグラウ ンドは空気によって散乱したスペクトル）。すると右上図のようなスペクトルが 得られる。このバックグラウンドを差し引いたスペクトルはXANESでも用いられる。

その２：次にスペクトルを拡大すると、わずかに波打った構造が見られるのが分る。 これから明らかなようにEXAFS信号はとても弱い。強力なX線源であるシン クロトロン光が必要になることが多い。 ここで、波打ったスペクトルの中心に線を引く・・・明らかにこの過程は任意性 を含んでしまうため、EXAFSがイマイチ信頼ならないという人も多い。

その３：引っ張った横線を横軸（このときエネルギーは波数に置き換えられる＊）に、 その横軸に対して波をプロットしたのが左の図。高エネルギー側になるにつ れ信号強度が弱まるので、波数の３乗を信号強度に乗することがおおい。Ｋ ＜３はXANESの情報（と思われる）なので切り捨てる。図の場合だとｋ＞１３くらいで信号 に明らかなノイズが見られるようになるので切り捨てる。残った部分をフーリエ変換すると・・・・擬動径分布関数（RDF、右下図）が得られる。 

＊このとき、吸収端エネルギーを０にする。ところが正確な吸収端エネル ギーも決定が難しいので任意性が混入する（ただしこれは後のカーブフィッティングで補正可能）


☆切り出すｋの範囲は目的によりけりだが、だいたいXANESとの境界は３くらい、上はノイズが見られない程度まで。しかし、第２近接まで調べたかったら、最低ｋ＞１２くらいは欲しい。
☆k³×χにするのは、ｋが大きくなるほどEXAFS振動が見えにくくなるため。なお、酸化物の場合は大抵ｋが大きいところのスペクトルは第二近接など遠い相互作用を表すことが多いので、第一近接を強調して解析したい時は、ｋの次数を小さくして解析するとよい。
☆RDFだけで結合の存在を議論するのはきわめて危険。大して広い領域でフーリエ変換している訳ではないので、フーリエゴーストとの区別が難しい。これはフィッティングすることで簡単に見極めることができる。
☆実際のボンド長とRDFで表れるボンド長が大きくずれるのは位相シフトのため。

その５：得られたRDFをEXAFS理論式（上の黄枠）でカーブフィッティングできる。 実際には、RDFでフィッティングするのではなく、適当なピークを切り取って 更に逆フーリエをかけて欲しいボンドの情報だけを含んだEXAFS信号を抽出したものでフィッティングする。なので、フーリエゴーストはあまり問題にならない。 （上の図ではMn-O, Mn-Mnの情報だけを切り取ってカーブフィッティングし ている） 配位数CN、DW因子、ボンド長などが得られる。なお、ここで後方散乱因子と位相シフトの情報をユーザーが与えなければならない（後述）。かつては標準サンプルから算出していたが、最近はFEFFのような第一原理多重散乱理論計算ソフトを使うことが多い。

フィッティングのマメ知識（中山の経験なので、正しいかどうかは分らない）
☆ピークの位置（横軸方向）に影響を与えるのは、ボンド長R、吸収端エネルギーE0、３次のキュムラントである。
☆ピークの強度（縦軸方向）に影響を与えるのは、DW因子、配位数CN、光電子の平均自由行程、４次のキュムラントである。
☆配位数CNを求めるのは至難の技である。ユーザーから与えて固定するのが一般的（もちろん研究目的による）
☆逆フーリエ信号でよい一致になるが、RDFでずれる場合→E0の見積もりがおかしいことが多い。
☆光電子の平均自由行程は、FEFFなどで見積もることが可能。


最後に、得られる情報の信頼性について（中山の個人的意見）。 ボンド長は多くの場合信頼できる DWもCNをあらかじめ固定値にしてある場合信頼できる。 CNはあまり信用ならない 更に解析時の任意性から、統計誤差よりも解析法による系統誤差が多くの 場合みられる。XRDのように絶対数として正確な結合長を得ることは難しい が、一連のシリーズ（例えば固溶体サンプル）のサンプル解析の場合は、比較値として有用である。

（後方散乱因子）
光電子が散乱される場合、散乱される方位によって散乱強度が異なる。これは位相のズレが小さい前方で強く、ズレが大きい後方で弱い。Aから出た光電子がBにあたってAに戻るような２体散乱の場合は、後方散乱だけを考えればよい（これは球対称ポテンシャルの場合）。散乱原子Bの原子種がなにか？ということで決定する。

（位相シフト）
EXAFSで得られるRDFは、実際のボンド長よりも短い。これは位相シフトの ためである。原子周りに形成されるポテンシャルは光電子波の位相をシフト させてしまう。この位相シフトは吸収原子Aと散乱原子Bの組み合わせによっ て決定されるので、RDF全体をシフトすればよいというわけではない。これはFEFFなどで簡単に計算することができる。

☆二体散乱の場合は、後方散乱因子と位相シフトの抽出は原子位置の座標によらない。だからFEFFなどで計算する場合は適当な位置に原子をおいて計算すればよい。
☆三体散乱以上の場合は、座標依存性がある。気をつけるべし。

散乱を考える際に、単純に吸収原子Aから散乱原子Bに光電子が散乱されAに戻るというパターン（２体散乱）を考えるだけではなく、上の図のような３体散乱の寄与も考えないといけないことがある。しかし、通常この寄与はきわめて小さい（きわめて対称性の高い配位環境でかつ原子振動が小さい場合を考えないといけない）。

☆この寄与が重要になるのは、上のようなA-B-Cが直線に近くなる場合である。Bでの前方散乱は比較的大きいので、A-Cの２体散乱の場合に影響を与える程度の散乱寄与が想定される。

回折法は同じ結晶サイトにある元素種を区別できない。上の図ではA-A,AB, B-Bの結合長は一定。 しかし、XRDは解析によって３D構造のかなり正確な情報が得られることがで きる。EXAFSは回折法と違い吸収元素周りの情報を見る（光電子の寿命が短いた め。）したがってA-A,A-B,B-Bの結合長の区別は比較的容易（といっても現 実には難しい。原理的にできるということ。）一方で、EXAFSは一次元情報し か与えない（多重散乱は本質的に3次元情報を含むが解析は非現実的）の で、結晶構造全体をそれだけで把握するのは困難。

特にXANESの第一原理計算による再現に絞って解説する。
前にも紹介したが、XANESは非占有軌道の吸収元素のLDOSを反映しているとした。だから、第一原理バンド理論計算などを使えば簡単にXANESを再現できそうなものだが、実際にはそう単純ではない。上に示したフェルミの黄金律により遷移確率W（つまり吸収スペクトル強度）は基底状態の波動関数ψi のみならず、内殻電子ホール状態を考慮した（つまり入射X線によって内殻部に電子ホールができた状態）波動関数ψf も考慮しないといけない。バンド理論を用いた場合、内殻ホールが周期境界条件の妨げになるので計算は非常に大変になる。
それではどうすればいいのかということで、散乱理論による計算がある。散乱理論では電子の波動関数を電子同士の散乱波の干渉として考えるものであり、XANESの場合は光電子と周囲の原子によって散乱される散乱波の和として記述される。結局、散乱理論もシュレディンガー方程式を解いて電子の波動関数を出す方法にしても、究極的には全く同じ解を与えるのだが、散乱理論の場合は球対称ポテンシャル（マッフィンティンポテンシャル）の仮定をすると圧倒的に計算の負担が少ない。（２体なら吸収原子A-散乱原子Bの結ぶ直線部だけを考えればよい）　なので、バンド理論計算では求めるのが難しいψf を比較的短い時間で求めることができる。ただし波動関数そのものの精度は散乱理論計算では低くなる。これは、マッフィンティンポテンシャルを用いていることと、たとえ波動関数をSCF計算で求めても、もともとタイト・バインディングな計算に基づいているので電荷の移動などが極端に小さく見積もられてしまうことに起因するのではないかと中山は考えている。

（おまけ）
第一原理多重散乱理論計算でよく使われている、FEFF８の見本ファイル（日本語翻訳版）

とりあえずココまで・・・